One-Point Perspective Explained

In my last post on perspective, I distinguished between linear and atmospheric (or aerial) perspective. Linear perspective is concerned with the geometry of parallel lines or edges as they recede in space, while atmospheric perspective is all about how colors shift as they travel through the air. What both types of perspective have in common is that they help us understand how the appearance of things changes with distance.
In the next few posts I want to focus on linear perspective, and clarify the differences between the three main types: one-point, two-point and three-point perspective.
What is One-Point Perspective?
As the name implies, “one-point perspective” refers to a point-of-view on objects that involves only one “vanishing point”. A vanishing point, as described here, is a theoretical location at which straight, receding, and parallel elements in a picture appear to meet. Think of railroad tracks stretching off into the distance – they appear to converge to a single point, even though they don’t in reality.
But when is it appropriate to use just one vanishing point? This is something that confuses a lot of students, but it’s actually quite simple. The number of vanishing points required for any given object in a picture is directly related to the object’s orientation to the “picture plane”.
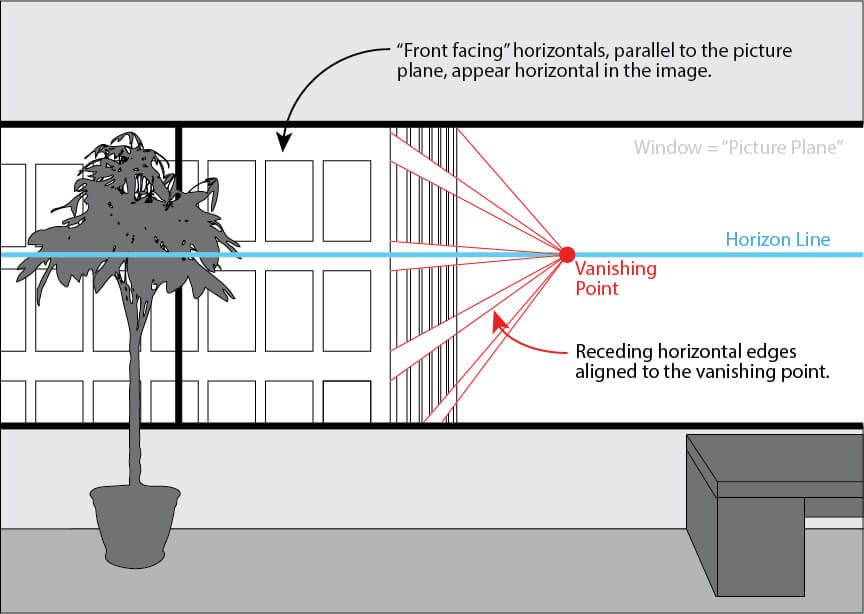
Remember, the “picture plane” refers to the surface of the image itself – when you’re drawing, think of the paper as if it were a window you’re looking “through” onto a scene that lies beyond it. The angle at which any given object is set relative to the “window” will determine whether it needs one, two or three vanishing points. For one-point perspective, objects must be oriented parallel to the picture plane – if we’re looking at a cube, there will be a “front-facing” plane that is at the same angle as the picture plane itself.
Imagine you’re standing in an office building, looking out a window. Across the street, there’s another building with windows facing back at you. Assuming these buildings are rectilinear (built with 90º corners) and are oriented parallel to one another, the windows of that other building will be parallel to the window from which you’re looking. For you, then, that other building would appear to be in one-point perspective.
So why do we need a vanishing point?
When you’re looking out the window at the building across the street, the edges of the widows facing you are parallel to the picture plane. As such they don’t need any vanishing point at all – they don’t recede away from you, and will thus appear to be parallel. Period.
But let’s imagine you can see a little bit of the side of that building. The windows on this side aren’t facing you at all, but are rather set at 90º to the window you’re observing from – the picture plane. The horizontal edges of those windows are receding away from you dramatically, and thus would appear to be aligned to a common point – the vanishing point.
That building across the street, then, would feature only one “set” of parallel edges that recede into the distance – the horizontal edges that are set at 90º to the picture plane – and thus only one vanishing point is required. This would be true for any rectilinear object set with a “front facing” plane that is parallel to the picture plane.
That, in a nutshell, is one-point perspective. Any rectilinear object with a front-facing plane that is parallel to the picture plane will require just one vanishing point in an image.
Next, I’ll discuss two-point perspective and the respective the orientation of objects relative to the picture plane.







Responses